气泡在受限空间的运动在微化工过程以及泡沫浮选、乳液过滤和流化床反应器等多种工业场合有诸多应用,气泡流在受限制的几何空间中运动是其主要特征[1]。 为了深入探究气泡在受限空间中的动力学行为,研究者常常使用2个平板之间形成的狭缝来模拟受限空间,这样的装置称为Hele-Shaw装置[2]。 在Hele-Shaw装置中,不同的气泡雷诺数可以通过倾斜装置并改变流体黏度来实现。 早期,大多数研究都集中在采用理论分析或者实验方法进行低雷诺数气泡流研究[3-7]。 而后,针对受限空间气泡流的研究,逐步从中雷诺数[8-10]扩展到了高雷诺数范围[11-13]。 然而,这些研究大多集中于固定狭缝宽度下受限空间内的气泡动力学。 Roig等[14]仅在1 mm狭缝宽度的Hele-Shaw装置中,研究了单个浮升气泡的形状和动力学参数等随气泡尺寸大小的变化。 Pavlov等[15]和Filella等[16]研究了受限空间横向宽度对气泡自由上升行为的影响。 解文潇[17]研究了受限尺度对气液传质的具体影响,并发现了受限尺度在1.5～2.1 mm之间存在能保留微尺度效应的临界值。 Xiang等[18]通过实验研究了壁面对浮升气泡动力学的影响,在受限空间中引入了垂直壁面,并控制它与气泡之间的相对距离来探究垂直壁面对气泡动力学的影响,证明了垂直壁的存在对气泡上升动力学的影响。 另外,针对浮升气泡的破碎及聚并等情况也进行了探究,Gaillard等[19]将实验与数值模拟相结合,探究了受限空间悬浮黏性流体中浮升气泡的破碎聚并演变情况及相关动力学规律。
但是,受限尺度作为对受限空间内流体动力学具有重要影响的一个因素,其变化对气泡受到的重力、表面张力、黏性力等相对大小的变化具有重要影响,而针对受限尺度的研究工作仍然鲜见报道。
本研究在不同狭缝宽度的Hele-shaw装置中,以CO2气泡在水中浮升的过程作为研究对象,采用CMOS高速摄像机记录气泡浮升过程,以探究受限空间狭缝宽度对浮升气泡动力学的影响。 通过定量测量和计算不同狭缝宽度下受限空间内CO2气泡的形状、浮升速度、偏转角以及相关的无量纲数,揭示浮升气泡动力学随受限空间狭缝宽度变化的规律,并对结果进行讨论。
1 受限空间浮升气泡流体动力学实验
1.1 实验装置及材料
本工作所采用的实验装置如图1所示。
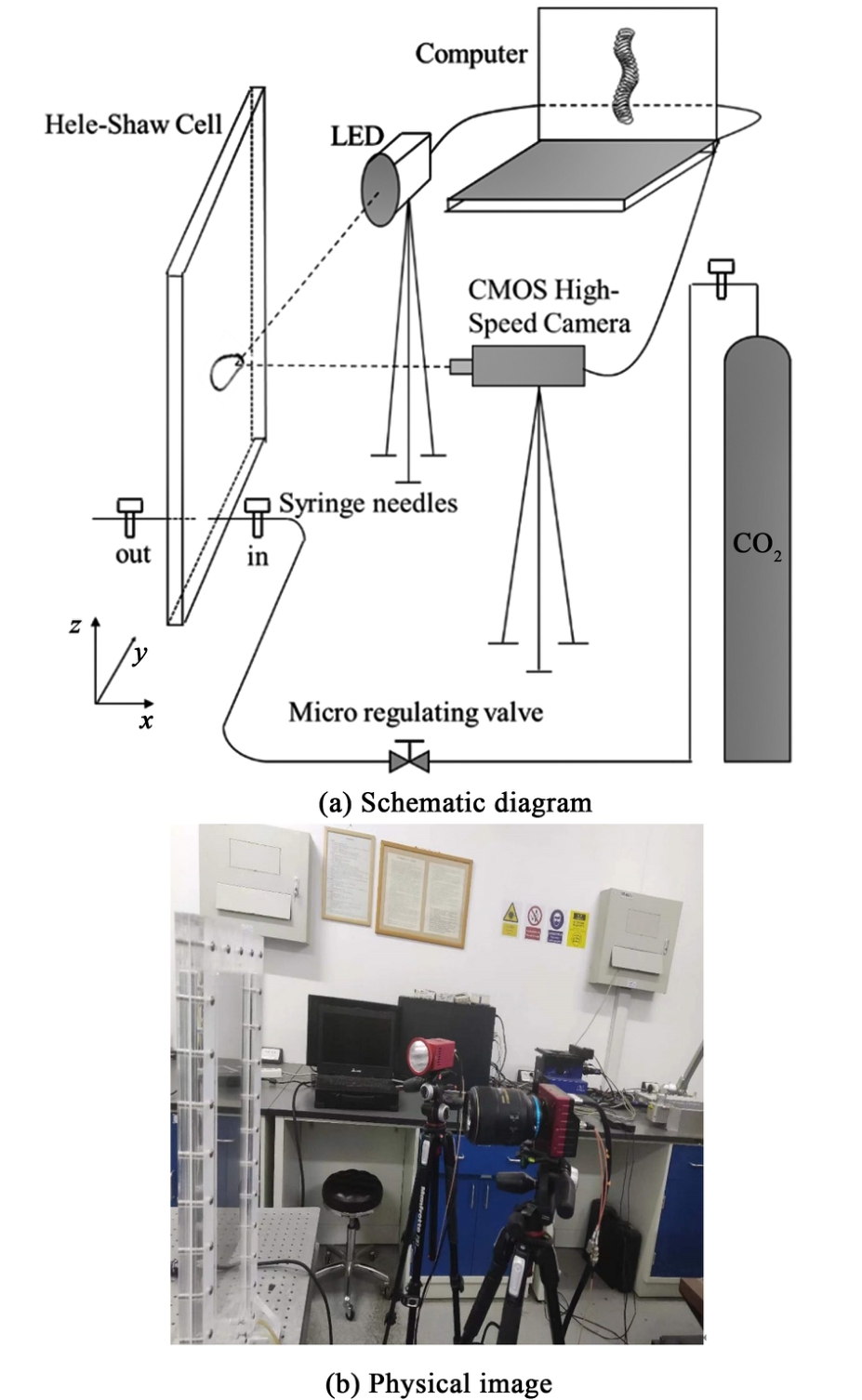
图1 Hele-Shaw实验装置
Fig.1 Hele-Shaw experimental set-up
如图1所示,实验装置包括3个部分,即液路系统、气路系统,以及光照成像系统。 在实验中,液相使用超纯水,气相为CO2。
液路系统包含Hele-Shaw狭缝装置和与进液口连接的针孔注射器。 Hele-Shaw装置由2块平行的PMMA(聚甲基丙烯酸甲酯)平板和夹在它们之间的亚克力密封垫片组成,侧边和底部的缝隙均用橡胶密封,形成2块板中间尺寸为高0.5 m×宽0.2 m的镂空区域,用于容纳超纯水和CO2气体。 垫片厚度分别为0.5、1.0、1.5和2.0 mm,以形成2平板之间实验所需的4种狭缝宽度尺寸。 在装置正面距离底端0.03 m的位置设有半径为4.82 mm的螺纹孔作为进液口。 超纯水需注入至进液口上方约0.6 m处,在装置顶部留有一定空间,防止在注入气体时液体溢出。
气路系统由从CO2钢瓶、通气乳胶管、微型调节阀、进气口和针孔注射器组成。 在距离Hele-Shaw装置底部0. 05 m的位置设置1个进气口,其尺寸与进液口相同,进气口用倒锥接头连接,再与乳胶管连接,在乳胶管的另一侧连接CO2钢瓶。CO2气体经乳胶管通道和进气口注入狭缝装置中形成气泡。 通过微型调节阀开度调节进气以控制气泡尺寸,气泡的投影面积当量直径范围为0～0. 02 m(体积当量直径范围为0～0. 01 m)。 为确保CO2气体纯度,实验前需要对管路进行CO2气体置换。
光照成像系统包括LED(脉冲光源)灯,用于拍摄记录气泡浮升过程的CMOS高速摄像机,以及用于处理数据的计算机。 高速摄像机(AcuteyeV4.0-1M-1900)分辨率为1 280 pixels×860 pixels,景深需大于狭缝装置的缝隙宽度,帧率为200 Hz,拍摄区域的大小可以观察到1～4个气泡振荡周期。 相机垂直于狭缝装置放置,其镜头上安装450 nm的高通滤光片,以滤除高频光线的干扰。 相机通过高速Coaxpress接口与计算机连接。 LED灯以一定斜角放置在Hele-Shaw狭缝装置的左后方,调整照射角度以气泡边缘的反光,并保证拍摄区域亮度均匀。实验过程中实验室内无其他光源,以减少光干扰噪声。 通过计算机控制,确保LED灯脉冲光源和高速相机的拍摄频率同步。 高速相机拍摄的图像储存到计算机中。 图像处理和数据处理均由MATLAB软件完成。
实验中使用的实验材料包括:超纯水、二氧化碳气体(体积分数大于等于99.99%)。 实验期间,温度控制在(25±0.3) ℃,以消除流体的热力学性质受温度变化的影响。 水和 CO2在25 ℃、101.325 kPa下的部分物性参数如表1所示。
表1 水- CO2 体系在25 ℃、101.325 kPa 下的物性参数
Table 1 Physical properties of water- CO2 system at 25 ℃ and 101.325 kPa
组分 ρ0 /(kg·m-3) μL/(Pa·s) σ /(N·m-1) D /(m2·s-1)CO2 1.976 1.51×10-5 0.004 34 2.02×103水997.047 0.000 89 0.072 1.91×109
1.2 实验过程与数据处理
实验中在Hele-Shaw装置中注入超纯水后;通过调节微型调节阀开度,在进气口针孔注射器处生成不同大小的单个CO2气泡;气泡经过观测区,CMOS相机记录下气泡浮升过程,每个气泡浮升过程结束后静置一段时间,待到液相完全静止后再通入下一个气泡。 实验中使用CMOS相机记录气泡浮升时的形状和位置,经过图像处理后得到不同大小的气泡轮廓。 图像处理过程:(1) 抓取单帧图像;(2) 提取图像平均背景;(3) 调整图像颜色;(4)去除平均背景图,具体如图2所示。 首先抓取单帧的原始拍摄图像,如图2(a);然后进行平均背景的提取,将气泡浮升过程中的每一帧图像进行加和后提取不变的背景部分,得到平均背景图,如图2(b);然后对每一帧图像去除背景图并得到清晰气泡轮廓,如图2(c);最后调整颜色使得气泡轮廓更加清晰,如图2(d)。 实验获得的不同尺寸大小的气泡如图3所示。
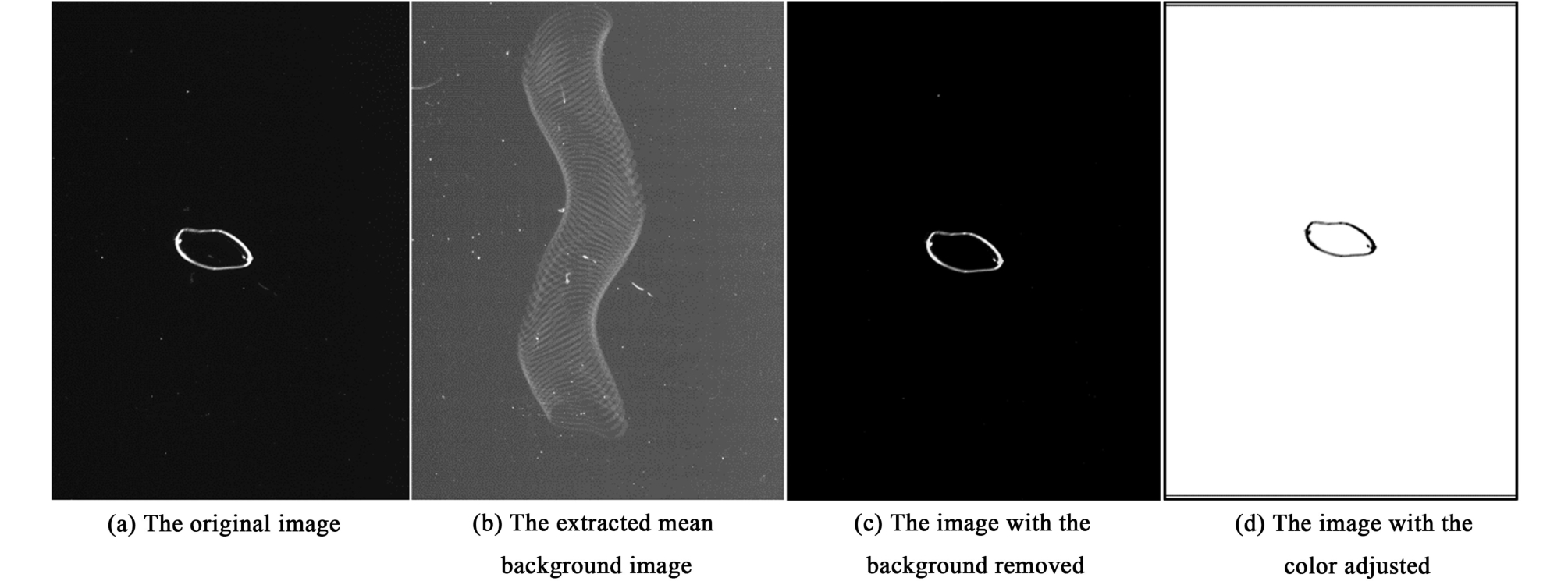
图2 单帧图像处理流程
Fig.2 Single-frame image processing workflow
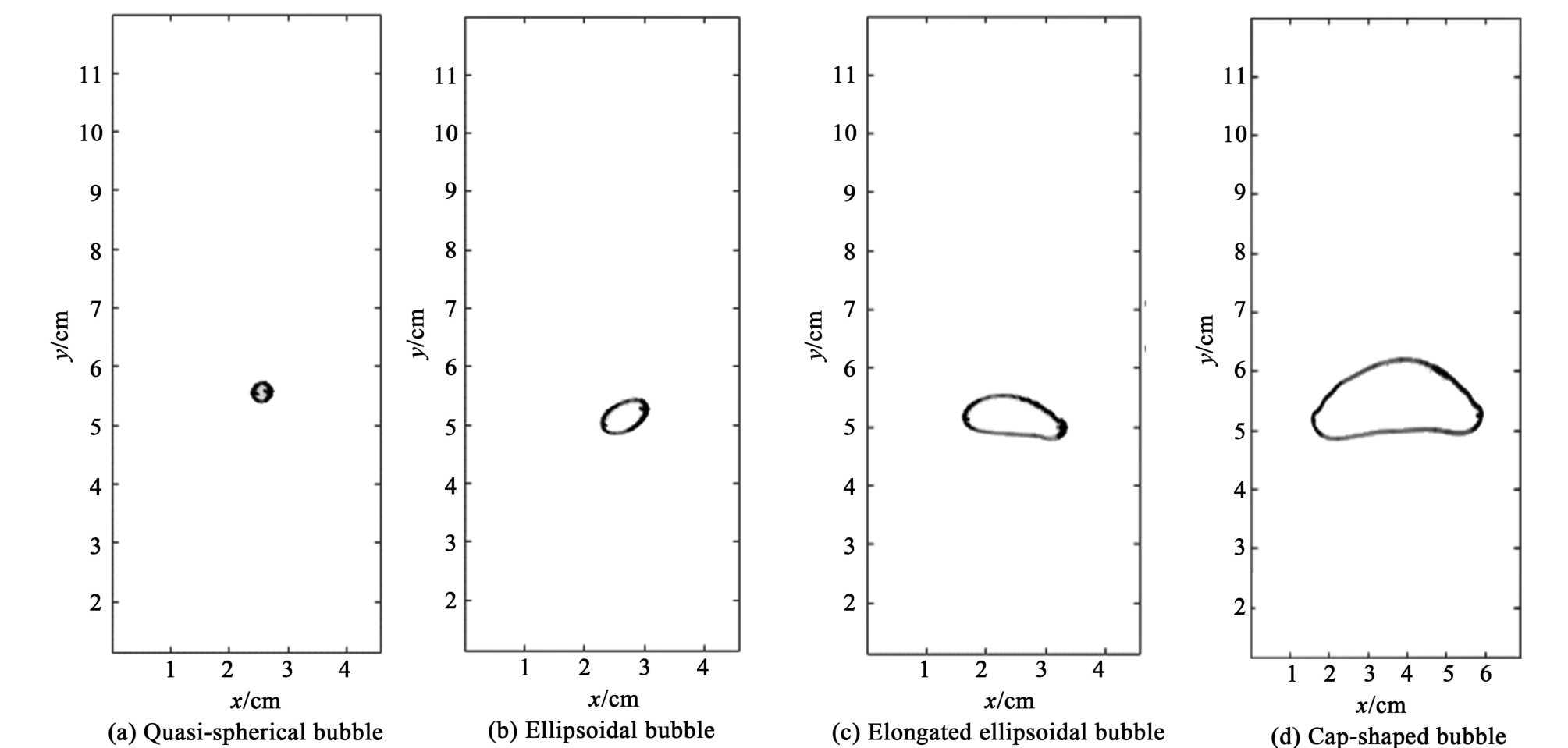
图3 受限尺度w =0.5 mm浮升气泡轮廓
Fig.3 Contours of rising gas bubbles under a confined scale of w =0.5 mm
2 结果与讨论
2.1 气泡形状拟合及动力学参数计算
将不同时刻记录的实验结果进行叠加,即可得如图4所示的气泡的浮升过程。
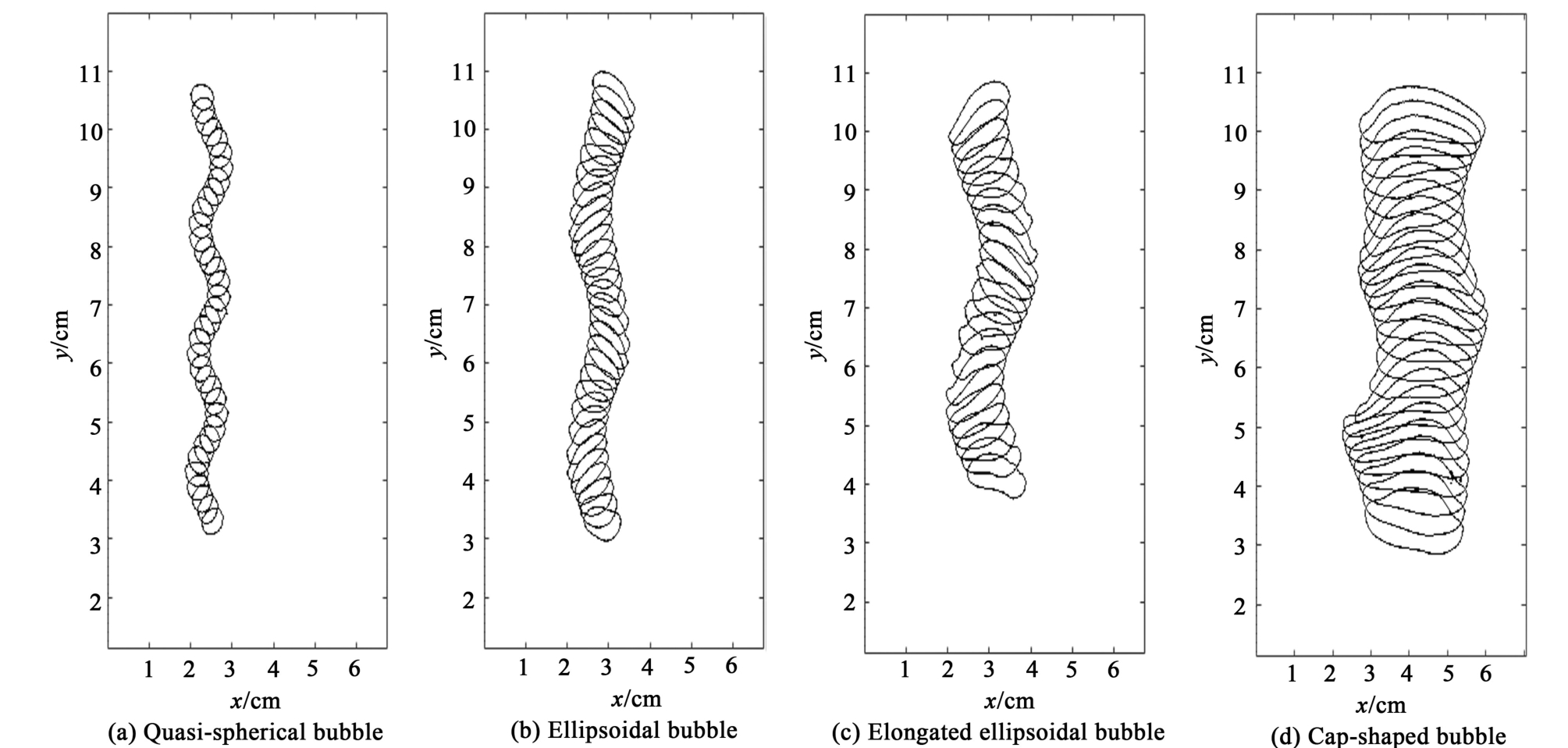
图4 受限尺度w =0.5 mm时不同尺寸大小的气泡浮升过程
Fig.4 Bubble rise dynamics under confined conditions with a characteristic length scale of w =0.5 mm
从图3可以观察到,随着气泡尺寸的增加,浮升气泡的形状依次呈现为类圆形[图3(a)]、椭圆形[图3(b)]、长椭圆形[图3(c)]和类帽形[图3(d)]。 为方便定量描述并计算浮升气泡的尺寸和形状,本研究将气泡轮廓拟合近似为等面积的椭圆形状,浮升气泡的轮廓与拟合的椭圆形状如图5所示,椭圆的长、短轴长度分别用a和b表示,气泡在壁面上的投影面积为S ,如式(1)所示。 本研究使用2种当量直径表示气泡的几何尺寸,分别为:(1)基于气泡的二维投影面积S计算的当量直径de,其定义如式(2),以及(2)基于气泡体积的体积当量直径d3D,其定义如式(3),其中w为狭缝宽度。
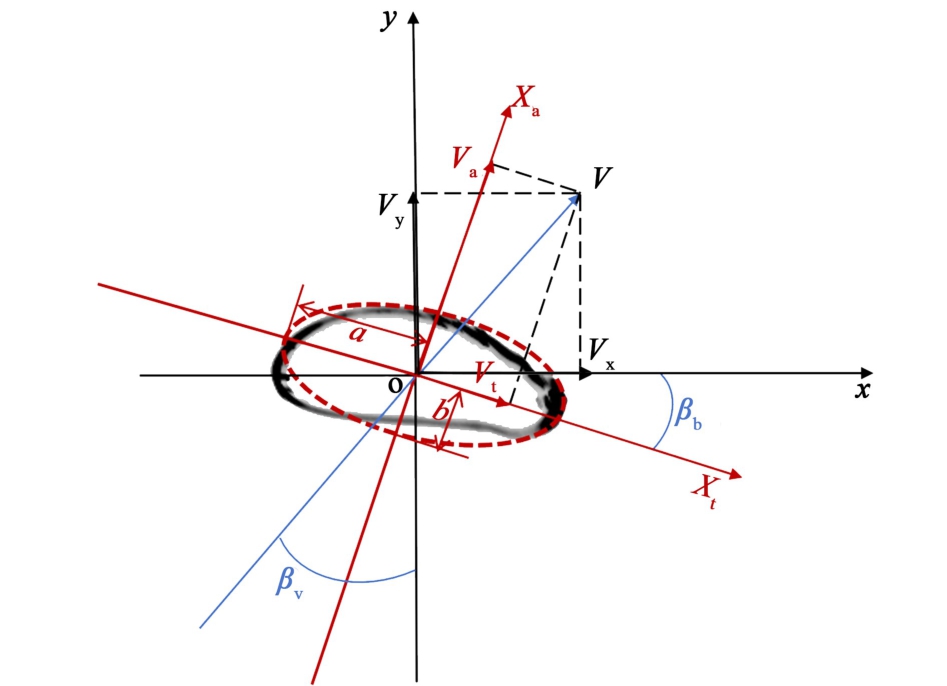
图5 气泡动力学参数
Fig.5 Bubble dynamic parameters
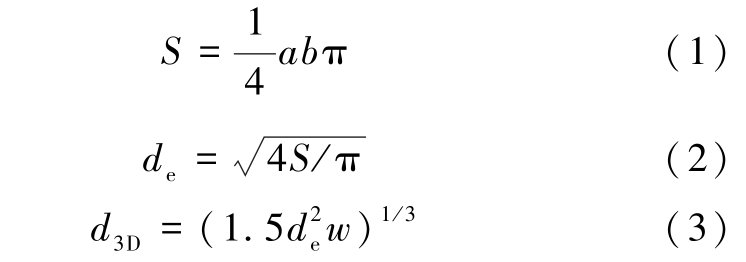
通过按时间顺序连续拍照的N帧图像,可以获得气泡的质心位置轨迹(xi,yi)(i = 1,2, …,N) ,其中xi和yi分别为气泡的质心的水平和垂直坐标。进而可得连续拍摄的2张图中气泡轮廓质心的移动距离(Δl)i(i = 1,2,...,N) ,以及气泡移动的瞬时速度Vi(xi,yi) = (Δl)i/Δt ,其中,Δt = 0.005 s是相机拍摄的间隔时间(拍摄帧率为200 Hz)。
如图5所示,本研究定义如下流体动力学参数。(1) 瞬时速度V ,描述气泡在液相中的移动速度,其在水平和竖直方向上分量Vx和Vy ;(2) 将瞬时速度V在拟合椭圆长轴和短轴上的分量Vt和Va ;(3) 气泡偏转角βb是拟合椭圆的长轴与水平方向的夹角,描述了气泡在液体中的倾斜程度;(4) 瞬时速度偏转角βv是气泡瞬时速度与竖直方向的夹角,反映了气泡运动方向的改变情况;(5) 漂移角βd是瞬时速度V与拟合椭圆的短轴之间的夹角;(6) 气泡的变形程度则由拟合椭圆的长短轴之比λb =a/b 。 这些参数的振荡情况反映了气泡在受限空间中的振动和摆动现象[16]。
通过观察图4可知,气泡的浮升过程呈现明显的周期性。 以狭缝宽度w = 1.5 mm下,气泡体积当量直径约为d3D = 0.002 7 m的实验结果为例,气泡动力学参数随时间的变化如图6所示。
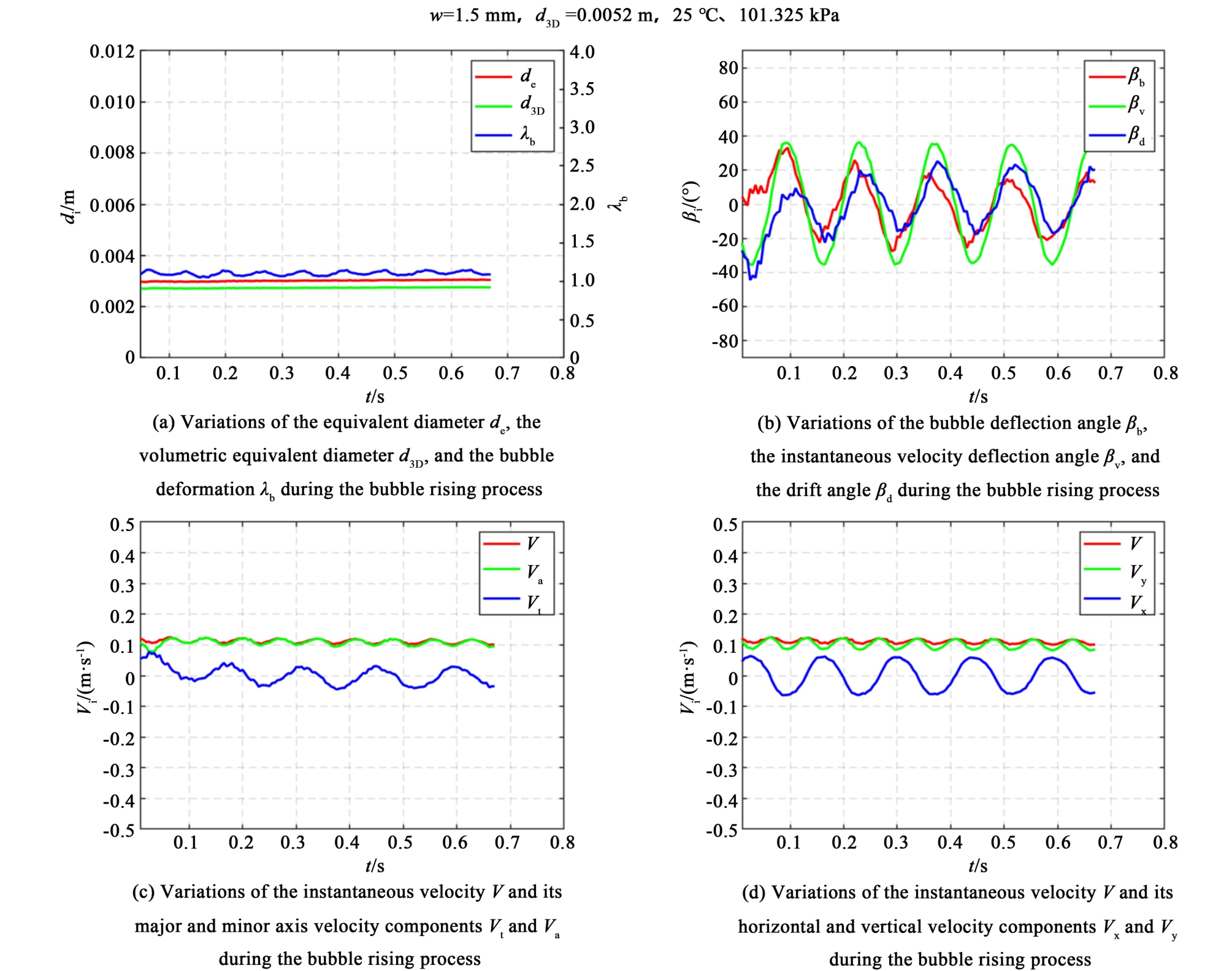
图6 单个浮升气泡的动力学参数随时间的变化
Fig.6 Variation of the dynamic parameters of a single rising bubble with time
为描述上述周期性,通过傅里叶级数拟合,可定义如式(6)～(11)参数。
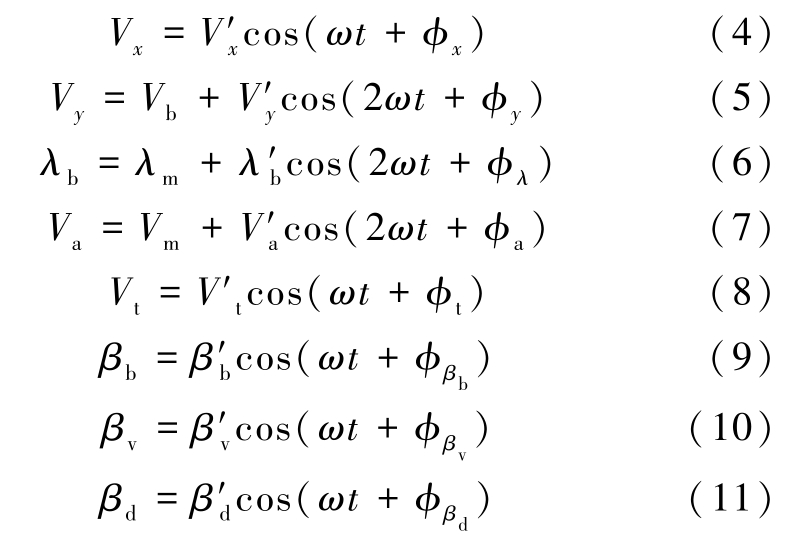
式(6)～(11)中:Vb是气泡的平均上升速度,即Vy的时均值; Vm是气泡在短轴上的平均速度,即Va的时均值; λm表示浮升气泡的平均形变程度,即λb的时均值; ω 是频率;
分别为各个参数的振幅, 
和
分别为各个参数的相位。
频率ω 的拟合结果如表2所示。
表2 ω 的拟合数据结果
Table 2 Fitting results of ω
参数 ω/ s-1 Vx 25.646 1 Vy 24.902 2 Va 25.471 8 Vt 25.236 8 λ b 24.941 2 β b 24.927 5 β v 25.478 4 β d 24.932 7平均相对误差/% 1.06
拟合得到的各个ω 的平均相对误差约为1%,说明上述方式拟合的误差较小。
2.2 不同尺度下动力学参数变化
重力和黏性力之比、重力和表面张力之比这2个无量纲数在气泡动力学中起着重要作用。 通常,重力和黏性力之比的无量纲数为阿基米德数
,重力和表面张力之比的无量纲数为
。 针对这2个参数,本研究重点在于考察其变化范围大小是否符合受限空间的要求,并继续研究气泡的流体动力学特征。 本研究的Ar范围在900～12 000之间,符合受限空间这一微过程对Ar的大小要求(100～15 000)。 本研究的Bo范围在0.37～12.33之间,也符合受限空间这个微过程对Bo的大小要求(0.1～140.0)。
由图6可知,气泡的当量直径在气泡浮升过程中变化较小,约为4%,表明气泡的大小在浮升过程中基本不变。 为更准确分析气泡浮升过程中的整体情况,本研究使用傅里叶级数拟合的各个气泡动力学参数的振幅和平均值来描述不同狭缝下气泡浮升过程的各个动力学特征。
2.2.1 气泡平均上升速度
不同狭缝宽度下受限空间气泡平均上升速度见图7。
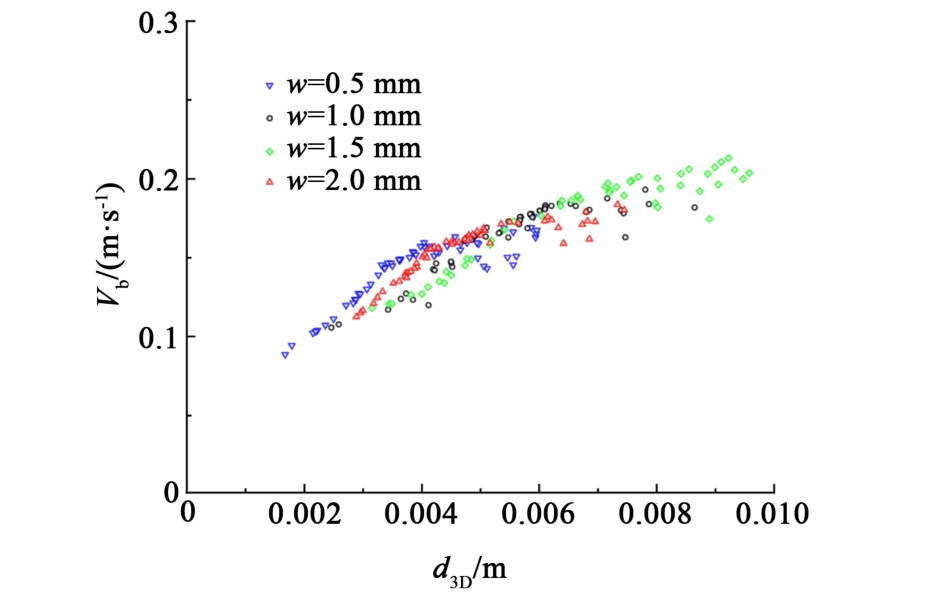
图7 不同狭缝宽度下受限空间气泡平均上升速度Vb
Fig.7 Average rising velocity of bubbles in confined space under different gap widths Vb
如图7所示,4种狭缝宽度下的气泡平均上升速度均随气泡当量直径的增大而增加。 在浮升过程中,气泡受到惯性力、表面张力和黏性力的共同作用。 气泡的惯性力与气泡的速度和质量成正比,表面张力约束气泡形状倾向于令气泡维持球形,而气泡受到的来自液体的黏性力会阻碍气泡运动。随着气泡尺寸的增加,惯性力逐渐增大,相较表面张力而言在气泡浮升过程中起主要控制作用,而液相黏度不变,黏性力变化较小。 因此,气泡当量直径越大,平均浮升速度越大,受到的惯性力也越大。而不同狭缝宽度下,当气泡体积当量直径接近时,气泡的平均上升速度随着狭缝宽度变化没有呈现出明显的变化。
2.2.2 气泡平均形变
不同狭缝宽度下体积当量直径d3D对气泡形变的影响见图8。
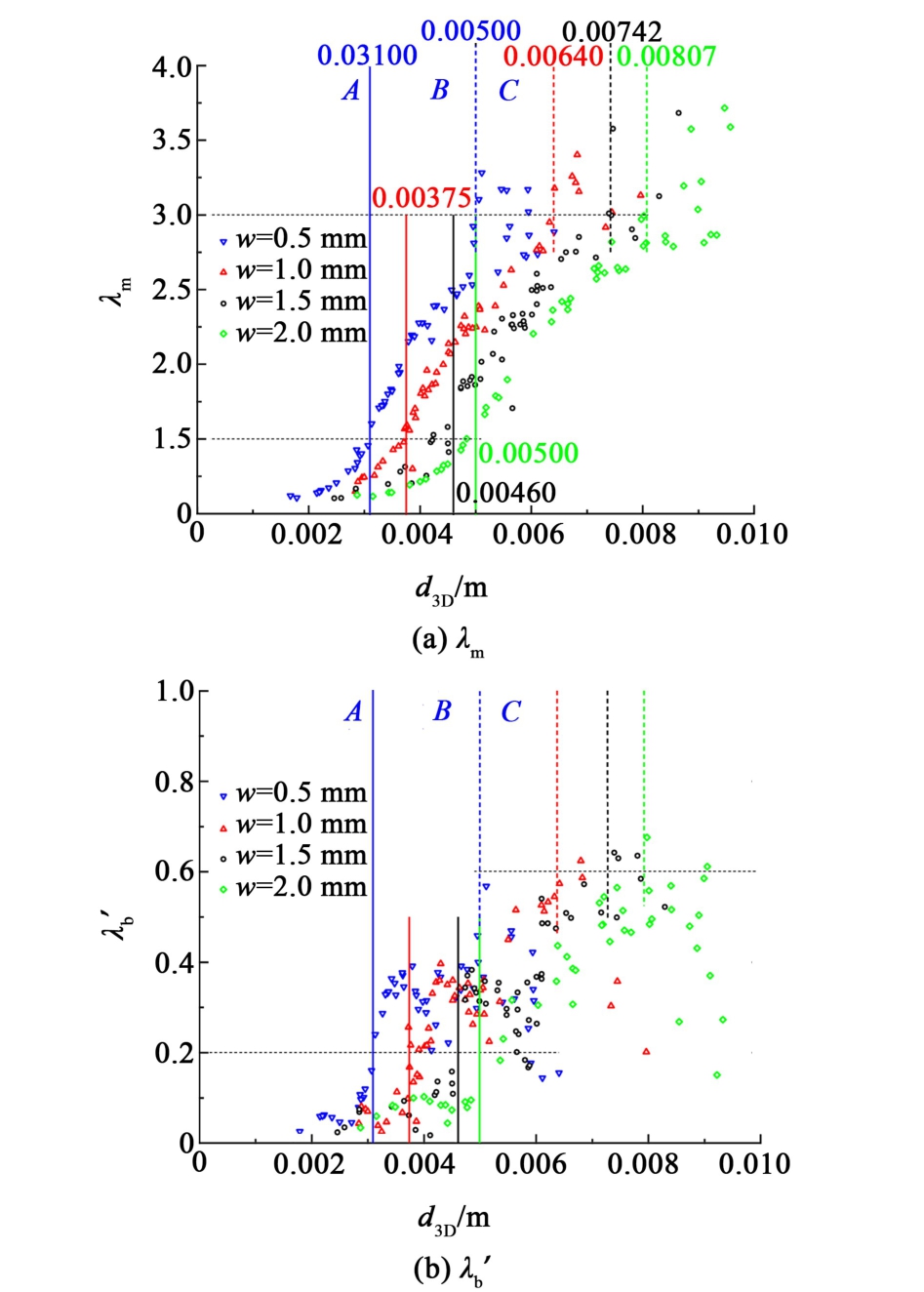
图8 不同狭缝宽度下体积当量直径d3D对气泡形变的影响
Fig.8 The influence of the equivalent volume diameter d3D on bubble deformation. under different gap widths
如图8所示,气泡的形变程度随着当量直径的变化呈现不同的变化趋势。 对于同一狭缝宽度下的气泡,可将当量直径坐标轴划分成A、B和C 3个区域。 4个狭缝宽度的区域A、B和C对应的具体区间标注在图8(a)中,后续其余气泡参数的区域A、B和C划分跟图8(a)相同。 如图8所示,以w =0.5 mm的狭缝宽度为例,在区域A,气泡的平均形变λm小于1.5,且其振幅λ′b小于0.2。 此时在该区域气泡为类圆形,如图4(a)所示。
在区域B,气泡的平均形变λm从1.5急剧增加到3,且此区域的振幅λ′b也从0.2增加到0.6。 此时,气泡为椭圆形或长椭圆形,形变振荡加剧,如图4(b)和图4(c)所示。
在区域C,气泡的平均形变λm分布较为分散且具有一定的随机性,这是由于该区域的气泡尺寸较大,上升速度较快,且动力学参数的变化不再具有稳定的周期性,继续使用傅里叶拟合会造成更大的误差。 但振幅λ′b整体仍随着气泡尺寸增大而急剧减小,此时气泡对应如图4(d)所示的类帽形,振荡较弱。 后续其余动力学参数的变化均基于这3个区域来分别讨论。
由图8(a)观察到,相同尺寸的气泡在较小的狭缝宽度下平均形变程度更大。 缝隙越小液体运动受到的壁面黏性力越大,对气泡上部的阻碍作用越强,而惯性力仍然令气泡保持上升的趋势,因此,在惯性力和黏性力2种相反方向的力的共同作用下,气泡被挤压的程度更高,气泡的长短轴之比越大,形变程度更大。
2.2.3 气泡角度
2 种偏转角,即βb和βv随着气泡尺寸的增大和狭缝宽度变化的情况如图9所示。
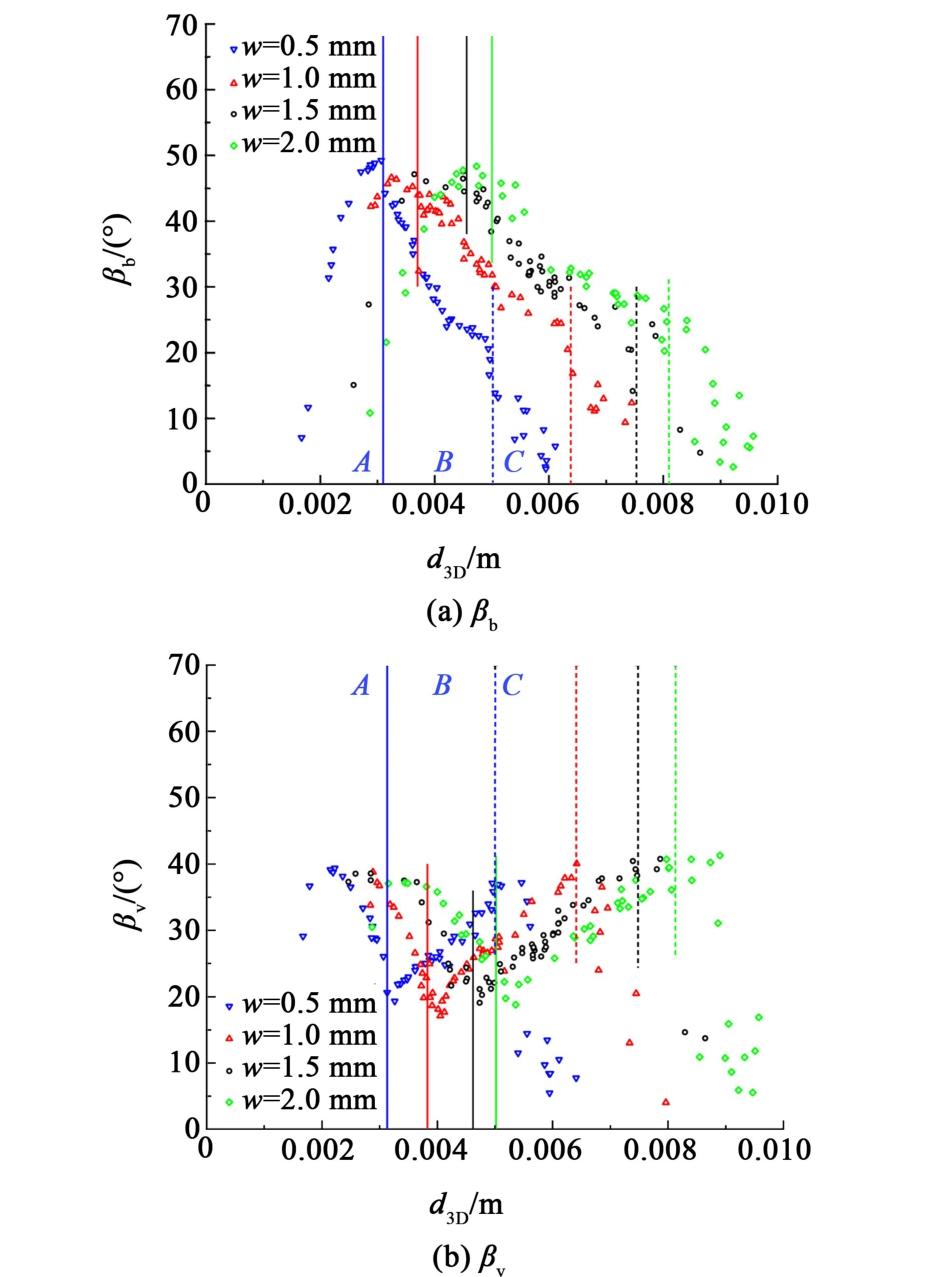
图9 不同狭缝宽度下气泡角度随体积当量直径d3D的演变
Fig.9 Evolution of bubble angles with volumetric equivalent diameter d3D at different gap widths
在区域A,不同狭缝宽度下的气泡偏转角βb随着气泡尺寸增加而急剧增大。 这是由于随着气泡尺寸增加,气泡开始出现振荡由直线上升转为之字形上升,此时气泡仍为形变程度较小的类圆形,并由图4(a)可知气泡本身相对于水平方向呈现出一定程度的倾斜。 在区域A中惯性力和表面张力共同作用于气泡,并且随气泡尺寸的增加表面张力的作用相对减小,惯性力对气泡浮升的控制作用增加。 另一方面在区域A,对于相同当量直径的气泡,随着狭缝宽度w减小,气泡偏转角βb增大,这是由于狭缝宽度减小,壁面对液相的阻力增大,进而导致气泡形变较小时就受到较大的液体周围的液体黏性力。 较大的黏性力对应的雷诺数更大,也更容易在气泡左右发生涡的周期性脱落,使得气泡在液体中的运动呈现之字形上升,又在表面张力作用下仍能保持自身形状。 而不同狭缝宽度下的速度偏转角βv在区域A先增大后减小,根据Roig等[15]的研究,其减小与壁面摩擦引起的涡量衰减有关。 而随着狭缝宽度的增大,区域A对应的当量直径增大,整体呈现右移的趋势,这是由于w越大,气泡的受限程度越低,由图8可知达到相同形变程度对应的气泡尺寸更大。
在区域B,不同狭缝宽度下的气泡偏转角βb随着气泡尺寸增大而减小,速度偏转角βv随着气泡尺寸增大而增大,这是由于随着气泡尺寸逐渐增大,惯性力增加并控制气泡浮升,限制了旋转振荡相对于平移振荡的幅度;另一方面,随着狭缝宽度w的增大,区域B对应的气泡当量直径增大,在区域B的某个范围内βb增大而βv减小,这是由于在区域B,形变程度加剧进一步影响气泡浮升, w增大使得壁面挤压减弱,形变较大的气泡受到的周围液体的黏性力减小,速度方向更接近于竖直方向,而周围液体的扰动增强,气泡倾斜程度更高。
在区域C,随着气泡尺寸增大,不同狭缝宽度下的气泡偏转角均急剧减小,这是由于气泡形变较大,但振荡减弱到微小;另一方面,随着狭缝宽度w增大,区域C对应的气泡当量直径增大,这是由于气泡受限程度减小,达到相同形变程度的气泡尺寸增大。
2.2.4 气泡振荡频率
为了进一步描述气泡浮升的周期性,本研究引入无量纲数St3D = ωd3D/Vb来进行表征,它表示气泡受到的惯性力与液体阻力的比值,而液体阻力与狭缝宽度有关,从而能够综合考虑受限尺度和振荡频率来分析气泡的周期性特征。
如图10所示,在区域A中,频率ω 随着气泡尺寸增大而减小,这是由于此区域气泡形变仍较小,受到的表面张力用以维持自身形状,黏性力较小且基本不变,随着气泡尺寸增大惯性力主导性增大,并且开始控制浮升过程,由图4可知气泡开始呈现之字形上升,并且尺寸增大气泡惯性增加,倾向于保持自身运动的趋势变大,气泡运动方向的改变就更慢,其运动方向完成1个循环所需的周期更长,频率更短。 另一方面在区域A对于相同尺寸大小的气泡,随着狭缝宽度w变大而频率和St3D都增大,这是由于缝隙变宽气泡受限程度降低,壁面对液相的挤压减弱,从而气泡受到的液体的黏性力减弱,气泡得以在更小纵向范围内完成周期运动,从而周期更短,频率更高, St3D增大。 从图10(b)可以看出,当气泡的体积当量直径进入区域B时,不同狭缝宽度下的St3D都基本重合在同一条直线上。 对应图10(a)可知,在区域B不同狭缝宽度的频率在数值上比较接近,约为25.858 0 s-1。 图7显示,气泡上升速度Vb受狭缝宽度影响较小。 结合St3D的定义式可知,当频率ω 和上升速度Vb都不受狭缝宽度影响时, St3D只与气泡当量直径有关。 因此,在区域B中,不同狭缝宽度下的St3D都重合在同一条直线上。但是,从图10(b)仍可看出,不同狭缝宽度影响着气泡进入线性区的起始当量直径,狭缝越小,气泡进入线性区的起始当量直径越小。 而在区域C,频率ω 和St3D的拟合误差很大,这是由于在此区域振荡微弱,气泡运动并不明显呈现出规律的周期性,继续按照傅里叶拟合参数会产生较大误差。
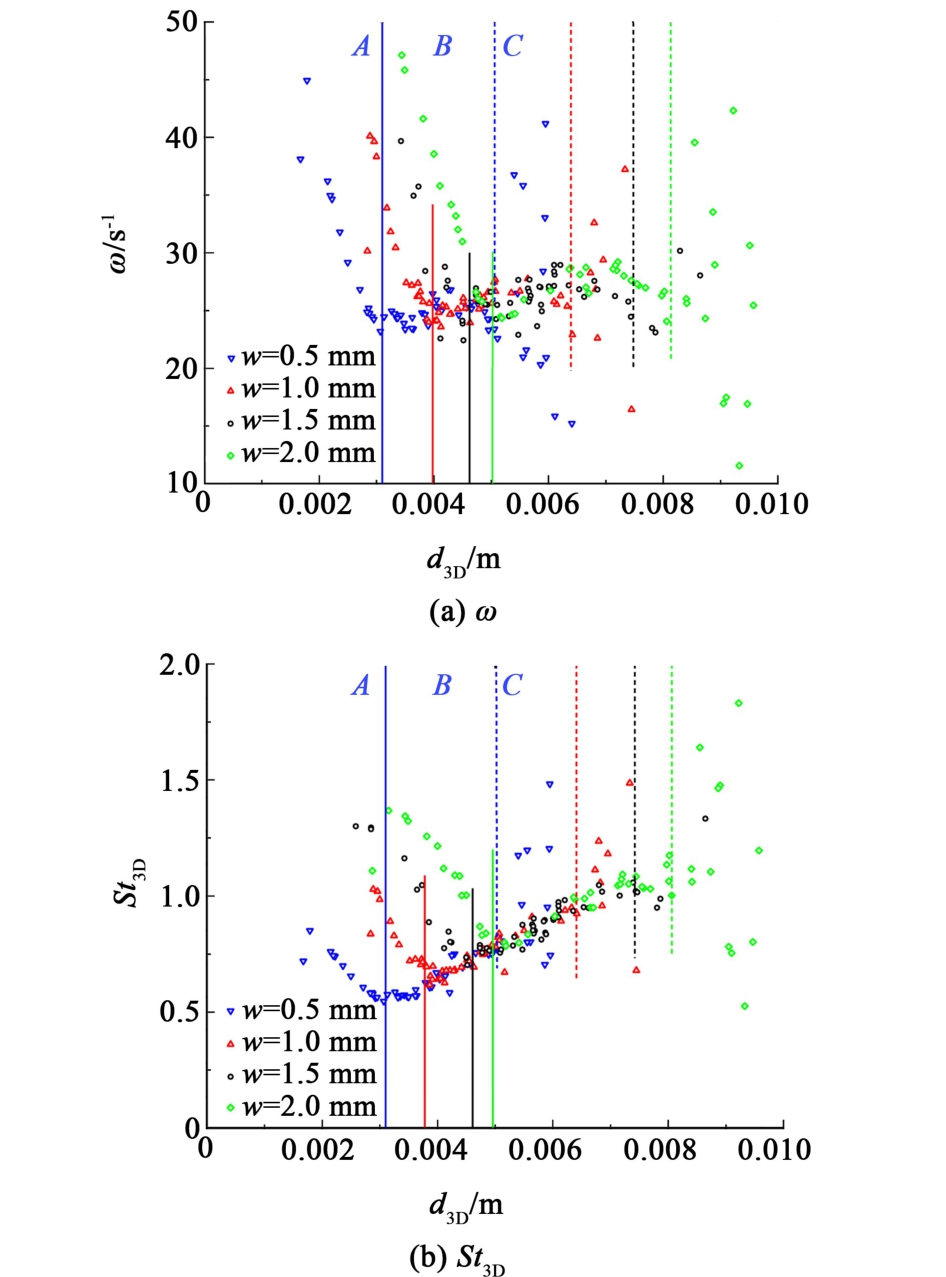
图10 不同狭缝宽度下气泡频率随体积当量直径d3D的演变
Fig.10 The evolution of bubble frequency with the volumetric equivalent diameter d3D under different gap widths
2.2.5 漂移运动参数
如图11所示,相较于在水平和竖直方向的分量,V′a/Vb比V′y/Vb更小,且近似保持不变,速度的振荡几乎集中于椭圆长轴上,因此将这种按照新的参考系来重新分解得到的气泡运动参数称为漂移运动参数,与之前的水平竖直分解方式相比,沿着拟合椭圆长短轴的分解更能反映出不同狭缝宽度下气泡动力学参数的变化规律。 后续重点讨论以拟合椭圆长短轴为参考系的气泡动力学
、βd等漂移运动参数变化情况。
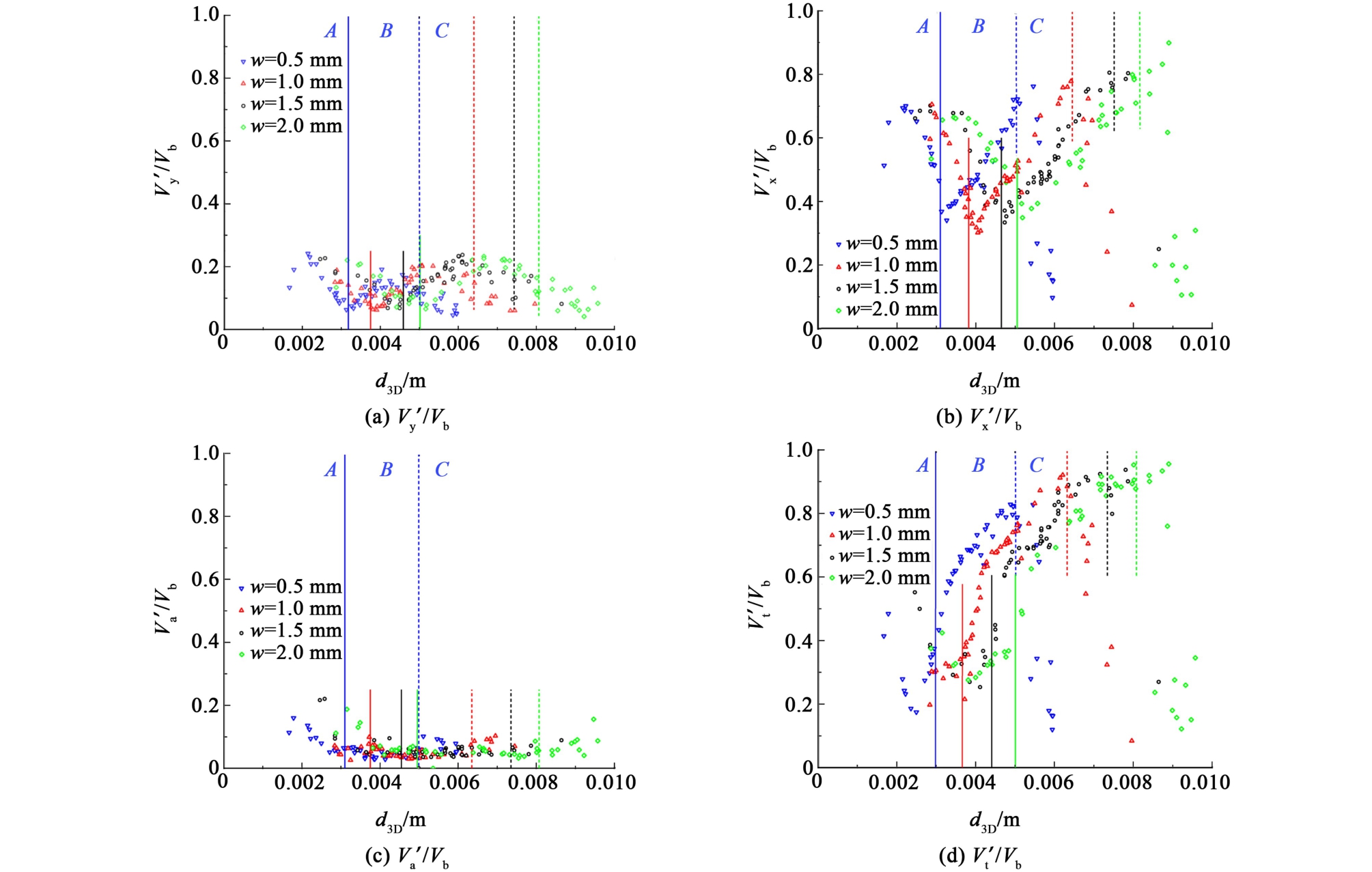
图11 不同狭缝宽度下2种参考系的速度振幅随气泡尺寸变化的情况
Fig.11 Variation of velocity amplitude with bubble size for two reference frames at different gap widths
如图11(c)和图11(d)和图12(a)所示,可以明显观察到,短轴速度分量振幅与长轴相比可忽略,而且漂移角βd和
的变化情况非常相似。
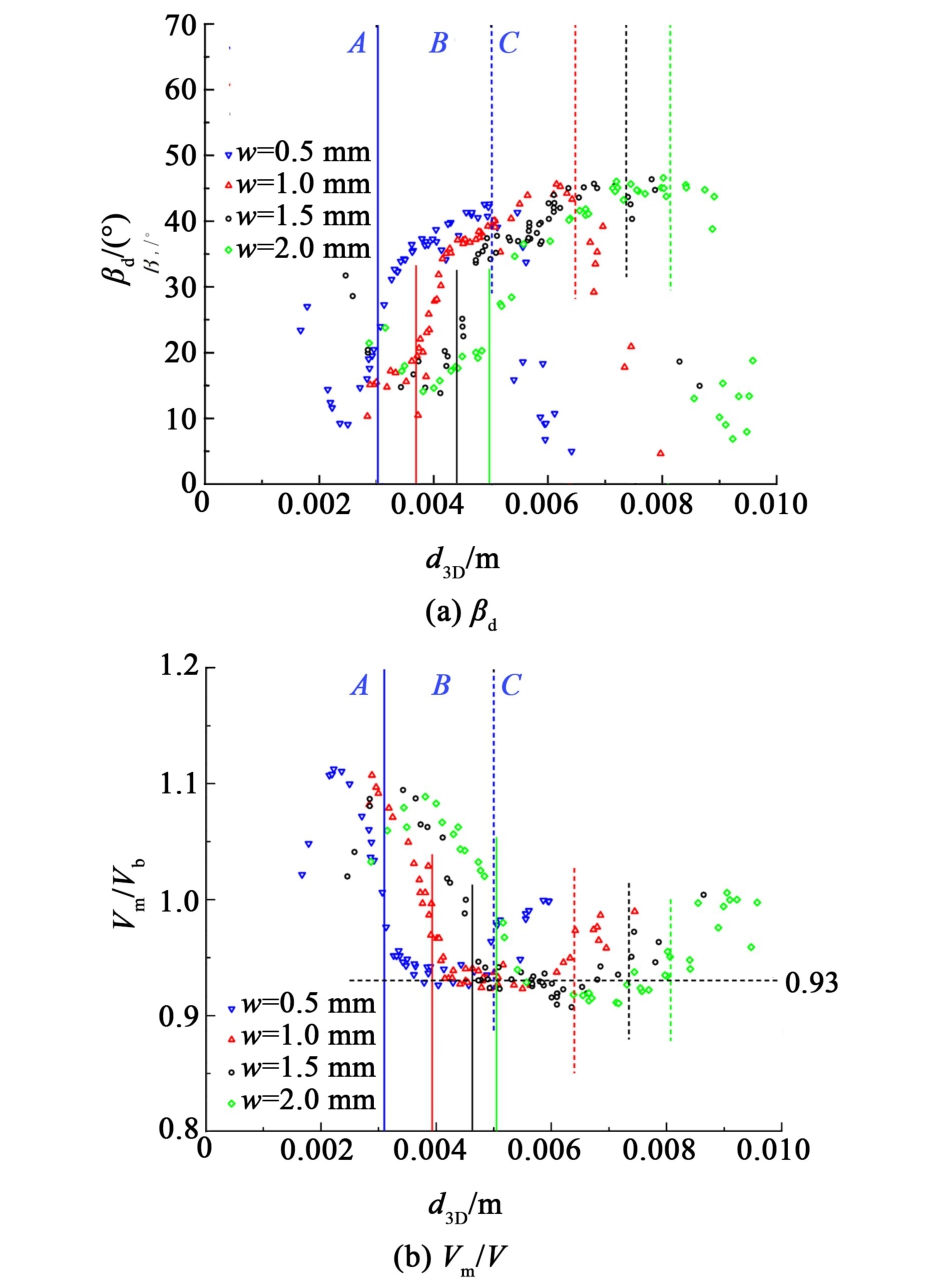
图12 不同狭缝宽度下气泡的漂移角β d和速度之比Vm/Vb随体积当量直径d3D的演变
Fig.12 The evolution of the bubble drift angle β d and the velocity ratio Vm/Vb as a function of the volumetric equivalent diameter d3D under varying gap widths
在区域A,随着气泡尺寸增大,长轴速度分量的振幅和漂移角的振幅总体上呈现先减小后增大的变化,这是由于在此区域气泡形变和气泡尺寸均较小,随着气泡尺寸增大气泡的上升速度也增大,受到的惯性力增大而表面张力减小,同时气泡运动开始出现周期性,气泡振荡较弱,动力学参数的振幅整体上有变化但并不大。 而随着狭缝宽度增大,区域A对应的气泡尺寸增大,相同振幅对应的气泡当量直径更大。
在区域B, 
和βd均随着气泡尺寸增大而急剧增大,在这个区域,气泡的形变程度加剧明显而且气泡上升速度也在增大,气泡振荡明显加剧,所以V′t/Vb和βd的振幅都急剧增大。 而随着狭缝宽度w的增大,区域B对应的气泡当量直径更大,相同振幅对应的气泡当量直径更大。
在区域C,振荡变得微弱,上述动力学参数振幅随着气泡尺寸增大急剧降低。
由图12(b)所示,进一步观察到不同狭缝宽度下的Vm/Vb在区域B的变化不大,且V′a/Vb在此区域约为5%,故短轴速度分量几乎是不变的, Vm/Vb约为0.936,与Roudet等[16]的结果Vm/Vb ≃0.92接近,说明本文的4个狭缝宽度下的浮升气泡在区域B均遵循这个比例定律。
我们进一步探究区域B的其他参数之间的关系。
如图13(a)所示,4个狭缝宽度下,相较于其余2个区域,在区域B, V′t/(Vbλm) 的值均基本不变(约为0.318 8),说明本研究的4个狭缝宽度下的浮升气泡的动力学参数在区域B均遵循这个关系;
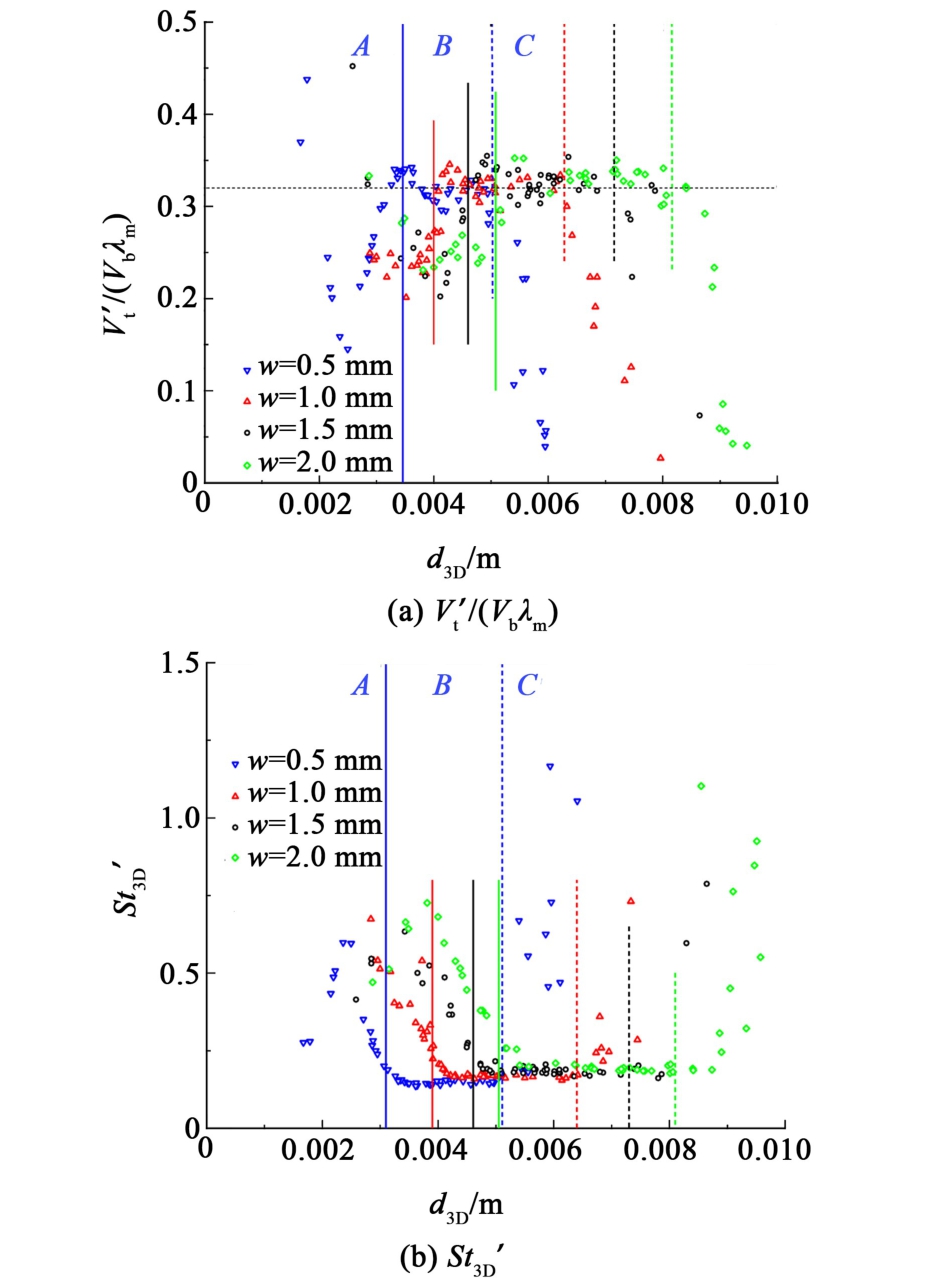
图13 不同狭缝宽度下区域B的比例定律
Fig.13 The scaling laws governing the proportion of Region B under varying gap aperture widths
另一方面,基于长轴速度分量的振幅
来考虑斯特哈尔数
,如图13(b)所示,相较于其余2个区域,在区域B均可视其为基本不变(约为0.184 3),即在区域B中,只要知道了气泡的体积当量直径,由之前的讨论可知ω 的范围可以确定,那么长轴速度分量的振幅V′t大致范围也可以确定,而已知V′t/(Vbλm) 也基本不变,根据气泡形状可以计算平均形变λm ,气泡的平均浮升速度Vb也可以确定。
故而说明4个狭缝宽度在气泡形变加剧的区域B中,均遵循上述定量关系,而在其余2个区域并未发现这样的规律。
3 结论
通过改变Hele-Shaw装置的狭缝宽度,研究了受限空间狭缝宽度,即受限尺度,对浮升气泡的动力学的影响。 结论为:(1)不同气泡参数的曲线均随着狭缝宽度变大而右移,呈现单调变化;(2)不同狭缝宽度下的气泡动力学参数随着气泡尺寸增大的变化不是单调的,需要分区域讨论,按照形变程度将气泡尺寸分为3个区域A、B和C;(3)不同狭缝宽度下的区域B具有相近的情况,气泡参数平均短轴速度Vm 、平均上升速度Vb 、长轴速度分量振幅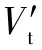
、气泡平均形变λm之间存在数个定量关系。 这些定量关系可以更好地说明浮升气泡的动力学参数之间存在的联系和狭缝宽度对浮升气泡的影响。对受限空间气泡动力学的深入研究具有重要意义。
应该指出,本研究的实验结果是在第一节的实验条件下得到的,在本研究条件下进行实验,结果表明受限尺度对气泡的运动情况及气泡参数存在显著影响,在设计受限空间化工过程时应作为重要参数予以考虑。
符号说明:
a—椭圆长轴,m;
b—椭圆短轴,m;
de—气泡平面投影面积当量直径,m;
d3D—气泡三维当量直径,m;
g—重力加速度,m·s -2;
S—气泡平面投影面积,m2;
St3D —斯特哈尔数;
t—时间,s;
V —气泡瞬时速度,m·s-1;
Vb —气泡平均上升速度,m·s-1;
Vm —气泡平均短轴速度,m·s-1;
Vx —气泡瞬时速度V的水平速度分量,m·s-1;
Vy —气泡瞬时速度V的竖直速度分量,m·s-1;
Va —气泡瞬时速度V的短轴速度分量,m·s-1;
Vt —气泡瞬时速度V的长轴速度分量,m·s-1;
w—缝隙宽度,m;
βb —气泡偏转角,(°) ;
βv —瞬时速度偏转角,(°) ;
βd —漂移角,(°) ;
λb —气泡形变程度;
λm —气泡平均形变程度;
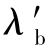—气泡形变程度的振幅;
σ —界面张力。
[1] DANOV K D, VALKOVSKA D S, KRALCHEVSKY P A. Hydrodynamic instability and coalescence in trains of emulsion drops or gas bubbles moving through a narrow capillary[J]. Journal of Colloid and Interface Science, 2003, 267(1): 243-258
[2] MARUVADA S R K, PARK C. Retarded motion of bubbles in Hele-Shaw cells[J]. 1996, 8(12): 3229-3233
[3] TAYLOR G, SAFFMAN P G. A note on the motion of bubbles in a Hele-Shaw cell and porous medium[J]. The Quarterly Journal of Mechanics and Applied Mathematics, 1959, 12(3): 265-279
[4] TANVEER S. The effect of surface tension on the shape of a Hele-Shaw cell bubble[J]. 1986, 29(11): 3537-3548
[5] ECK W, SIEKMANN J. On bubble motion in a Hele-Shaw cell,a possibility to study two-phase flows under reduced gravity[J].Ingenieur-Archiv, 1978, 47(3): 153-168
[6] MAXWORTHY T. Bubble formation, motion and interaction in a Hele-Shaw cell[J]. Journal of Fluid Mechanics, 1986, 173:95-114
[7] BISWAS K G, DAS G, RAY S, et al. Mass transfer characteristics of liquid-liquid flow in small diameter conduits[J]. Chemical Engineering Science, 2015, 122: 652-661
[8] KELLEY E, WU M. Path instabilities of rising air bubbles in a Hele-Shaw cell[J]. Physical Review Letters, 1997, 79(7):1265-1268
[9] BUSH J W M. The anomalous wake accompanying bubbles rising in a thin gap: A mechanically forced Marangoni flow[J]. Journal of Fluid Mechanics, 1997, 352: 283-303
[10] BUSH J W M, EAMES I. Fluid displacement by high Reynolds number bubble motion in a thin gap[J]. International Journal of Multiphase Flow, 1998, 24(3): 411-430
[11] BOUCHE E, ROIG V, RISSO F, et al. Homogeneous swarm of high-Reynolds-number bubbles rising within a thin gap. Part 1.Bubble dynamics[J]. Journal of Fluid Mechanics, 2012, 704:211-231
[12] DAVIES R M, TAYLOR S G. The mechanics of large bubbles rising through extended liquids and through liquids in tubes[M]/ /Dynamics of Curved Fronts. Amsterdam: Elsevier, 1988:377-392
[13] COLLINS R. A simple model of the plane gas bubble in a finite liquid[J]. Journal of Fluid Mechanics, 1965, 22(4): 763
[14] ROIG V, ROUDET M, RISSO F, et al. Dynamics of a high-Reynolds-number bubble rising within a thin gap[J]. Journal of Fluid Mechanics, 2012, 707: 444-466
[15] PAVLOV L, D′ANGELO M V, CACHILE M, et al. Kinematics of a bubble freely rising in a thin-gap cell with additional in-plane confinement[J]. Physical Review Fluids, 2021, 6(9): 093605
[16] FILELLA A, ERN P, ROIG V. Oscillatory motion and wake of a bubble rising in a thin-gap cell[J]. Journal of Fluid Mechanics,2015, 778: 60-88
[17] 解文潇. 受限空间内浮升气泡与液体间传质行为实验研究[D]. 天津: 天津大学, 2022 XIE Wenxiao. Experimental study on mass transfer behavior between floating bubbles and liquid in confined space[D]. Tianjin: Tianjin University, 2022 (in Chinese)
[18] XIANG S, JIAN Z, KHERBECHE A, et al. Experimental study of single bubble rising near vertical wall in Hele-Shaw cell[J].Chemical Engineering Science, 2022, 255: 117647
[19] GAILLARD A, KEELER J S, LAY G L, et al. The life and fate of a bubble in a geometrically perturbed Hele-Shaw channel[J].Journal of Fluid Mechanics, 2021, 914: A34